1507. The Laurel – Hardy Story

Laurel and Hardy are two famous movie characters of the 50’s. They are well known for their differences in weight as you can see in the picture on the left. In case you don’t know them, I should add that Laurel was the lighter guy. In their younger days Laurel and Hardy used to play with a strange seesaw and when the seesaw was at a stable position Hardy was always nearer the ground. We will now investigate a two-dimensional version of their seesaw.

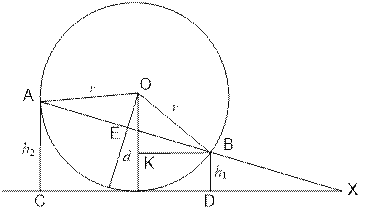
The seesaw that Laurel Hardy used can be considered as part of a circle of radius r, as shown in the picture on the right (Filled gray and having the shape of a D). Hardy sat on point B (rightmost point of the seesaw) and Laurel sat on point A (Leftmost point of the seesaw top AB). d = EF is the distance between the midpoint of line AB and arc AFB. So E is the midpoint of line AB and F is the midpoint of arc AFB. MN is the ground of the seesaw, which is horizontal with the plane. BD = h₁ is the distance of Hardy from the ground. Your job is to find out the distance of Laurel (denoted by h₂ = AC) from the ground.

Input. First line contains an integer n (0 < n ≤ 1000), which indicates how many sets of inputs are there. Each of the next n lines contains a single set of input. The description of each set is given below:

Each line contains three integers r, d and h₁ (10 £ r £ 100, 5 £ d £ r, 5 £ h₁ £ d). The meanings of these integers are given in the problem statement above.

Output. For each input set produce one line of output. This line contains the serial of output followed by a floating-point number, which indicates the value of h₂. This floating-point number should be rounded up to four digits after the decimal point. Look at the output for sample input for details.

Sample input	Sample output
2 10 10 10 10 7 6	Case 1: 10.0000 Case 2: 8.0342

SOLUTION

geometry

Algorithm analysis

From triangle OEB: OB = r, OE = r – d, sin ÐEBO = (r – d) / r.

From triangle OKB: OB = r, OK = r – h₁, sin ÐKBO = (r – h₁) / r.

Find ÐKBA = ÐKBO – ÐEBO.

From triangle OEB: EB = , AB = 2 * EB.

From triangle BDX: BX = BD / sin ÐDXB = h₁ / sin ÐKBA.

Find AX = AB + BX.

From triangle ACX find the answer: h₂ = AC = AX * sin ÐDXB.

Algorithm realization

Read the number of test cases t.

scanf("%d",&t);

for(i = 0; i < t; i++)

{

Read the input data for current test.

scanf("%lf %lf %lf",&r,&d, &h1);

printf("Case %d: ",i+1);

Compute b = ÐKBA = ÐKBO – ÐEBO = arcsin(r – h₁) / r – arcsin(r – d) / r.

b = asin((r - h1)/r) - asin((r-d)/r);

If b = 0, then points A and B are at the same distance from the ground (line CX) and h₂ = h₁.

if (b == 0.0)

{

printf("%0.4lf\n",h1);

continue;

}

Compute AX = 2 * + h₁ / sin ÐKBA.

ax = 2 * sqrtl(r*r - (d-r)*(d-r)) + h1/sin(b);

Find the answer h₂ = AX * sin ÐDXB (ÐDXB = ÐKBA) and print it.

h2 = ax * sin(b);

printf("%0.4lf\n",h2);

}